Lets hope that the year of the Ox will bring health and propserity back to the World !
Happy Chinese New Year
Category: Pentominos Programming Problems
Final Pentominoes Post: the code works !!
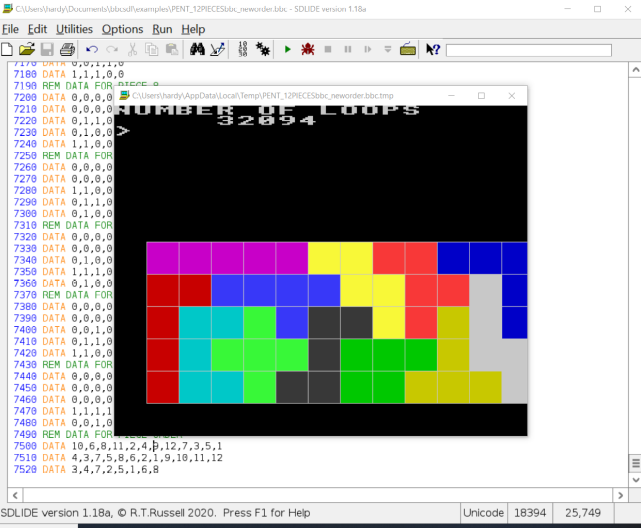
Probably two weeks have passed since the initial failure of the original code logic to find a solution to fit all 12 Pentominoes into a 12 by 5 space. After ironing out a few bugs in the initial code, it did manage to find solutions for 5,8,10 and one time 11 pieces. However, even after running overnight, it failed to find a solution to the full 12 piece problem. I think the code is sound, it’s just that it relies on chance to find a solution and with the large number of iterations required to solve for 12 pieces it is just very unlikely to randomly be selected. Eventually it should work – I might run this exe on an AWS cloud based PC which can easily be left to run for a week if required.
The following modifications in the logic resulted in success (and some very spaghetti like code.)
- The piece order can now be read in from data statements, and in the future can be made random. Normally I start off with the “X” pentomino since there are fewer possible starting solutions (this piece has no reflections or rotations).
- For a given starting position for piece1 the code evaluates all possible legal positions for piece2,3,4…and so on until no more solutions are found. It then moves back onto the next position of the previous piece until a full solution is found for all 12 pieces. This way ensures that the solutions tested run from left to right, so this algorithm has a kind of natural packing whilst still being a brute force search. If left to run “forever” this code should eventually find all 1010 possible solutions for the 12×5 fitting problem.
This version of the code has already produced two out of the 1010 solutions with the same starting position for the X piece. I’m happy that my initial goal has been achieved, within the timeframe assigned. Remaining tasks (which probably do not merit further posts) are:
- truly random piece order, starting with user decided starting piece.
- bring in piece reflections
- Only reflect or rotate pieces which need it (at the moment all pieces are rotated which is a bit wasteful.
- Simplify code logic and introduce more subroutines to reduce duplicated code.
- More advanced “hole checking” routines to reduce some spurious interim solutions
- Algorithm to weight solutions to proceed to faster convergence.
- Version which will find all possible solutions.
- Bring in some AI algorithms
- Recode in Python or something other than BASIC.
Watch this space for any progress reported !
Disappointing !!
Lots of progress in the past week, and quite a busy week, but no cigar as yet in terms of a full solution to the 12 piece pentominoes problem. The various modifications are summarised as follows.
- Using DATA statements to define each piece.
The use of data statements was a quicker way of defining each piece in terms of a 5×5 array. In the future then the piece can more easily be rotated and its edges can be automatically detected for fitting inside the chosen box. This modification was tested on the 5×5 test data.
- Rotating Each Piece using Matrix multiplication
Having defined each piece as a matrix, we can then use rotation of a matrix by 90 degrees to generate more possible pieces for each defined Pentomino. The logic used to rotate a matrix by 90 degrees was to take the matrix transpose (for which a function is already defined) and then swap matrix columns. I admit I found this solution on the internet, but I still havn’t used the internet to find possible solutions for the main Pentomino problem I’m trying to solve.
Finally I added some routines to remove spare rows and columns from the rotated matrix such that the Pentomino is always packed into the bottom left corner.
- Testing Solution on 5 pieces in 5×5 square
I had to change some small parts of the original logic, but the extension to rotating pieces worked well in terms of finding several additional solutions of this particular 5×5 problem.
Two such solutions are shown and generally less than 200 iterations were required.
- Extension to 12 pieces
The solution so far is restricted in that it doesn’t allow for reflections of the pieces, just rotations. The order of the pieces is fixed to either running from 1 to 12 or 12 to 1. However it still should be possible to find a solution. Since the end of the month was approaching, I quickly coded up the remaining 4 pieces and let the code iterate away at the entire problem I was trying to solve.
No solution found !! Disappointing !!
I think I left the code to run for 50,000 iterations before I gave up and tried it again. Still no joy. Then I found some small errors in defining the actual pieces, but each time I tried the code I obtained no solution. Unless there is a bug in the code, I’m pretty sure this brute force search should find one of the solutions …eventually…. but maybe I’m just not leaving it to run for long enough. Time for some thinking….
Pentominoes: First Working Code
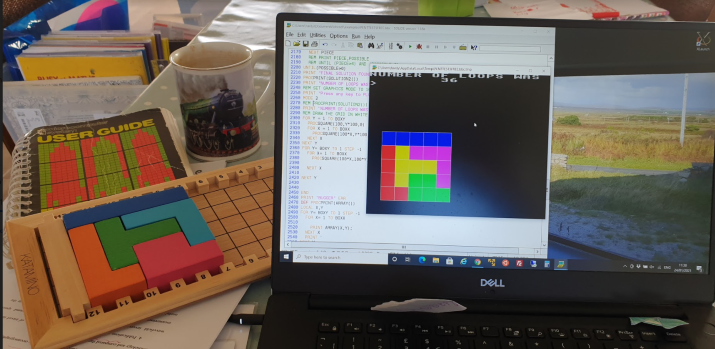
It works !! Moving on from the previous starting code.
- I added a routine which would select one of the possible solutions from those available. All possible solutions are found and stored. Currently we select a solution for each piece randomly, later we might select the possible solutions one by one or high grade the solutions based on some algorithms we might define to obtain quicker convergence. At the moment once a solution is selected for a given piece, we move onto the next piece. If no solution is found for the next piece then we go back to the beginning again. A final solution, and associated graphics, is only produced once a solution is produced for all 5 pieces. Currently when we go back to the beginning we restart the searches each time and carry on with random selections. This is a bit wasteful, but it will work eventually.
- I started with 3 pieces, with the first hard coded, and then checked the code such that solutions were found in the order 1,2,3 and 1,3,2. Next we freed up the first piece and tested orders 1,2,3 and 3,2,1. Ultimately all 12 pieces must be tested in random orders.
- Next we made the code slightly slicker, and moved onto four pieces. Interestingly, despite previous testing, this uncovered a bug in which piece 3 found no solutions but the code could carry on and find a solution for piece 4. The logic had to be changed slightly to get around this problem resulting in some messy, but working code.
- The final extension to 5 pieces was straightforward as was adding in the final screen graphics.
My 5 pieces are currently hard coded into orientations which I know will produce a solution for testing. The next level of complexity will be to add in rotations and reflections of the pieces. At the moment the piece shapes are hard coded – it would be possible to carry on with this method and hard code reflections and rotations for each piece. There are 63 possible combinations. I plan to investigate a more efficient way of storing the pieces in arrays and then using array manipulations to achieve the rotations where required. This will be the result of the next post.
Remember you can subscribe to the posts with a link to the right of the main post. I’m also experimenting linking these posts to my linkedin profile.
Pentominoes: First Code Attempts
As I’ve mentioned, the actual coding is slightly ahead of the blog pages, because I’ve spent ages trying to configure the blog and the online Tonnta Store. All this while supervising two recalcitrant daughters for zoom school during covid lockdown.
I generally write code in chunks, testing each section and building in more detail. Well, I havn’t coded anything in 20+ years, so maybe I shouldn’t generalise ! The first code hardcodes the first piece, an “L” shape and runs a loop around a 5×5 box to fit in the second piece. Arrays are used to store both the solution and each piece with a trial being produced by adding the arrays together. There is code to check that the piece doesn’t fall outside of the array of the solution (in this case 5×5. I’m still thinking I might pad the solution area to avoid these checks, but then that would give me a much bigger search box which could be wasteful. I also wrote a text printing subroutine for debugging purposes since it would be quicker than the graphics shown earlier. The code cycles through possible solutions printing various diagnostic information together with the current position of the pieces. I used the wooden blocks that I bought to help visualise and check the various solutions that the code produced. In the above diagram the two pieces overlap (1+1)=2 so this would be rejected.
The next modification was a routine to check for isolated holes and thereby reject possible solutions. It searches around the potential hole (in this case top left) and if the hole is completely isolated then the potential solution is rejected. This is the first stage in “high grading” the possible piece positions. I’ve yet to decide whether this type, or further position grading will be required. It may be that too many checks will slow everything down – such a solution will be “found out” soon enough because the last pieces will ultimately not fit and the code will have to go back to the beginning anyway !
By the way, you can subscribe to this blog using the link to the right of the posts.
More on Pentominoes
I was thinking about making a set of the 12 Pentominoes for my kids using salt dough or lego. However during lockdown we only have a few lego sets here and the pieces are tied up. I couldn’t bring myself to dismantle part of the Death Star for pieces, even though my daughters have removed most of the guns and fitted the Death Star out as bedrooms for Harry Potter lego minifigures. A few have commented on my linkedin post on different ways they have made Pentominoes in the past.
I found the following pictured game set online at Cogs the Brain Shop in Dublin. There are some quite nice things on the website and the delivery was fast, only a few days. My daughters went to work to find a solution…..and I was using the set to help visualise algorithms for my computer solution. Would we find a solution manually or my computer first ? The race was on…..
Graphics
As in all good projects, I decided to start with the final display, that is the graphics. I was able to locate the BBC microcomputer user guide in my loft. My guide is dated 1982 and acknowledges, among others, Richard Russell who wrote the BBCSDE interface that I decided to use in the previous post. The user guide contains a list of BBC BASIC commands and covers basic graphics with some sample programs including a classic Moon Lander game. I started by flicking through the book.
It didn’t take to long to write a simple BASIC code that would plot the grid and display Pentomino pieces in different colours. The code itself is quite useless, but it was a good start and will come in handy for displaying solutions (assuming I find any) and debugging algorithms that aim to fit the pieces together. I also found that the Teletext graphics mode contains several of the Pentomino pieces and that it is possible to define more as characters. An algorithm could probably be made directly using graphics commands and direct memory addressing or just based on the colours. However I decided against that approach since it would be difficult to port to other codes in the future.
Introduction
I discovered the existence of Pentominoes quite recently while reading Arthur C Clarke’s “Imperial Earth”. Checking out the Wikipedia page I discovered that these were a quite recent concept (well, 1953) and had originally been made popular by Martin Gardener in his Scientific American column. Somewhere in the loft I have Gardener’s “Mathematical Puzzles and Diversions” which probably includes a section on Polyominoes, of which the Pentomino is but a 5 cell subset. Another famous subset is the Tetromino which was used in the video game Tetris. I think in the loft I have an old gameboy with Tetris, I wonder if it still works. I recall I bought Gardener’s great book to learn more about hexaflexagons which I had seen featured in the 1974 Royal Institute Christmas Lectures by Eric Laithwaite. Somewhere in the same loft (the loft gets quite a few mentions but I can’t hyperlink to it), I also have a letter from Laithwaite. Since I was only 9 at the time I probably didn’t understand most of the concepts of the lectures or the books, but they probably had an influence on my scientific career. Someday soon I might seek out the book and see if I understand it now.
I introduced the Pentominoes to my children (8, 10) using coloured paper squares in pretty much the same way that Clarke introduces them in his books to the fictional child, Duncan. In 15 minutes my children had found more of the possible 12 shapes (ignoring reflections and rotations) than I did. The paper versions I had made, even when improved with light cardboard and blu tack didn’t really work out that well, but did provide a few hours of non screen related diversion for the family after covid lockdown school had finished.
Later, whilst out walking the dog, I decided that it would do my brain good to write a computer program which searched for solutions to a Pentomino type problem. Of course there are doubtless whole websites dedicated to such containing algorithms, discussions and free programs to download. However, for once, I wanted to develop something from scratch like we used to before the internet ! I also decided to use BBC basic which is also a throwback to the 80’s for me (these is also an old BBC microcomputer in the loft).
I first setup a website in 1999. However once I set it up I couldn’t think of much to populate it with that would be of interest to anyone else. I think I added song lyrics of tunes I could play on the guitar, a few pretty photos and a thought for the day section. I imagine this is what early Facebook pages looked like and it turned out that I didn’t have many thoughts. In 2001 I changed the site into xsgeo.com which contained some basic training material, but I was never very much attracted by the blogging concept. When I setup this store to enable sales of training courses and other services the blog part came for free, since I used WordPress as the basis for the ecommerce part of the website. I had the idea that visitors to the website could use the blog posts to file problems or curiosities with the seismic data which I (or other users) could then comment on. The purpose of this particular blog, though, is to record my thought process and progress towards the goal of writing Pentomino code which will find a solution to a given problem and provide appropriate graphical printout.